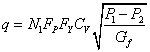 (1)中
(1)中 N1—数字常数(见表1);
Fp—管道几何形状系数;
Fy—流体阻塞流系数;
Fr—雷诺数修正系数;
Cv—阀流量系数;
P1—阀入口绝对压力;
P2—阀出口绝对压力;
G1—液体比重。
2、气体流量的计算公式
气体或蒸汽的流量基本公式是
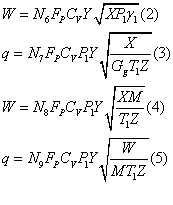
式中
Y—气体膨胀系数
Fx—绝热修正系数
K—气体绝热系数;
X—压降比系数,系压差与入口绝对压力之比,X=ΔP/P1 (8)
XT—压降比系数,也就是膨胀系数,X的最大值;
γ1—在入口条件下气体重度;
M—气体分子量;
T1—绝对温度;
Z—气体压缩系数。
数字常数N
|
N |
q |
W |
Cv |
P1P2 |
Dd |
v |
γ |
|
N1=1 =0.865 |
Scfh m³/h |
|
gpm gpm |
Psia bar |
|
|
|
|
N2=890 =0.00214 |
|
|
同上 |
|
in mm |
|
|
|
N3=1 =645 |
|
|
同上 |
|
in mm |
|
|
|
N4=17300 =76200 |
Scfh m³/h |
|
同上 |
|
in mm |
Cst cst |
|
|
N5=1000 =0.00241 |
|
|
|
|
in mm |
|
|
|
N6=63.3 =27.3 |
|
1b/hr kg/h |
|
Psia bar |
|
|
1b/ft² kg/m² |
|
N7=1360 =417 |
Scfh m³/h |
|
|
Psia bar |
|
|
|
|
N8=19.3 =948 |
|
1b/hr kg/h |
|
Psia bar |
|
|
|
|
N9=7320 =2240 |
Scfh m³/h |
|
|
Psia bar |
|
|
|
表中单位符号解释:gmp=美国加仑/分;psia=绝压磅/时²;bar=巴;in=时;cst=厘斯;1b/hr=磅/时。
上各个公式使用的单位和相应的数字常数N值列于表1,下面详细地解释公式中各个修正系数的物理意义和计算方法。
二、流量计算的实用公式
ISA标准提出的计算公式采用了许多系数对阀流量系数Cv进行修正。但是直接应用计算公式还是比较麻烦。因此美国Driskell在此基础上推导出许多实用计算公式,考虑到使用的单位有公制和英制,实用公式仍然使用数字常数。
1、液体流量计算
液体通过阀的流动呈紊流情况。液体不发生闪蒸和空化现象时,它的实用基本公式
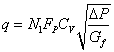 (1a)
(1a)
该公式与以前计算公式相比,仅有一个管道几何形状系数Fp,ISA标准规定测定调节阀额定Cv值,阀必须安装在与阀体法兰相同口径的笔直管道上,如阀两边有渐缩(扩)管等零件相连接、就要用Fp修正阀的Cv值。如阀两边直管道与阀公称通径相同,则Fp=1.0。Fp可用实验方法确定,也可用下式计算。
式中
Cd—阀相对容量系数;
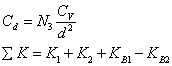 (3a)
(3a)
其中K1和K2分别表示入口和出口管道的阻力系数,KB1和KB2分别表示入口和出口渐缩(扩)管的柏努利系数(即流束面积变化所引起的阻力系数的变化)。若渐缩管和渐扩管的规格相同,则KB1=KB2。即流束横截面积向它原来的方向变化时,入口渐渐管上的压力损失会在出口渐扩管上得到恢复。若规格不同,或一侧有而另一侧无渐扩(缩)管,式(2a)应有一个柏努利系数。
标准规定:渐缩管和渐扩管规格相同时,
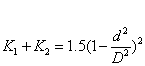 (4a)
(4a)
只有渐缩管
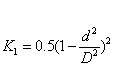 (5a)
(5a)
只有渐扩管
例1 已知液体为海水,比重G=1.2,流量q=1500gpm,P1=75psia、P2=65psia,管道直径D=8"。
计算:由式(1a),可求出Cv
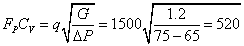
若选一台6"蝶阀,它的额定Cv=720。因为d=6"
所以
由式(2a)得
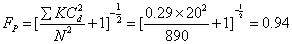
这台蝶阀安装后,实际Cv变成
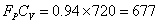
结果表明阀在70~80%开度上工作,能满足工艺设计的要求(520/677=76%)。
2、粘性液体流量的计算
式(1)仅适于紊流状态的牛顿液体。实际上,粘度较大流体或阀Cv较小,流动可能呈非紊状态。因此,标准引进一个雷诺数系数Fr来修正Cv,并规定用试验方法确定FR。实验证明FR与阀的雷诺数Rev的关系曲线如图1所示。Rev的实用公式是
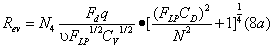
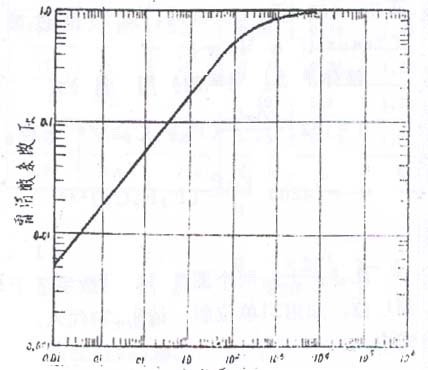
图1液体流量计算的雷诺数系数Fr
式中
γ—动力粘度系数,百斯(cst);
Fd—调节阀结构型式的修正系数,标准规定V型球阀和单座调节阀为1.0,流体流动呈两个平通路的阀,如双座调节阀和蝶阀为0.71;
CD—调节阀和管道的容量系数,CD=Cv/D²,D为管道内径;
FLP—液体压力恢复系数FL和管道几何形状系数Fp的组合,这要比单独计算F和Fp来得方便,很显然,若调节阀与管线直径相同,则Flp和D就分别等于FL和FLP实用计算公式是
此主题相关图片如下:
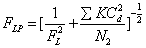
式(8a)方括号内分式的数值表示“趋近速度”。除全开的球阀和蝶阀之外,数值很小,可忽略不计。
从图1可知:Rev>3300时,流动呈紊流,Fr=1,Rev<100时,流动呈层流,流量与压力降成正比,而不是与
液体流动呈层流的实用计算公式是
注意:上面两个圆括号内的数字适于英制单位,如用SI单位制,请用173代入。
式中
ц—液体运动粘度系数,百泊(CP);
Fs—液体层流流动系数,它是阀本身影响流量的各个因素的一个综合系数,不受渐缩(扩)管的影响,各种阀Fs计算公式为:
例2 已知牛顿液体比重Gf=0.90,T1=70°F,粘度μ20000CP,P1=85psia,P2=65psia,流量q=52gpm,管道直径D=3",(40"规格管子)。
计算:(1)假设流动呈紊流,由式(1a):
(2)假设流动呈层流,由式(10a):
若选一台60°转角蝶阀,由表2查得Fs=0.92。
所以
。这台蝶阀在70%开度上工作,可满足工艺设计要求。
3、过渡流;液体过渡计算实用公式是
关键问题是怎么知道流动是过渡流,Driskell提出了一个简单方法。先假设流动呈紊流,再假设流动呈层流,分别求出Cv值,然后求出这两个Cv值之比η,η>20流动为紊流,η<0.46为层流,0.46<η<20为过渡流。最后,从表3上查出相应的Fr。若流量或压降是未知数,也采用这种解法。
例3已知液体比重G=1.0粘度µ=2000CP,V型球阀内径d=2",管道直径D=3",P1=74psia,P2=62psia,额定Cv=100,Fl=1.0,Fp=0.83,只有渐缩管。
